Aurora: Matrices are from Venus

Do not worry about your difficulties in Mathematics. I can assure you mine are still greater..
-- Albert Einstein

Introduction

Matrices seems to be some of the most misunderstood concepts of games programmers today. One does not even need to go into quaternions to find that just regular 4x4 matrices are surprisingly misunderstood. Even more frighteningly, people fresh out of college sometimes have what amounts to no working knowledge how they work and what you use matrices for, let alone can they talk about them. This is not being elitist, smug or any other term you could come up with, I really honestly don't think it's too much to ask for a games programmer to be able to go from one space to another (without using a library function)? I would be hard pressed to find any field within games programming, where you didn't need to know about math and matrices.

Even if you're doing 2D pixel games you still have to know about matrices since you need to transform back and forth the actual pixel values in different colorspaces. And guess what, you do that typically with matrices.

You're a network programmer, and you need to figure out why the network packets are making the characters drift ever so slightly, but it's extremely hard to catch and debug. So you employ my favourite debugging method, visual debugging. This might involve drawing some debug graphics on screen about the known gamestate of the characters, their interpolated velocity vectors, the last known vectors etc. And this is all in 3D of course, and you will probably need to transform the velocity vectors into localspace to catch and color drifts in different directions (e.g. left, right).

Mathematics

Let us for a moment forget about the sordid details that a computer and floating point math brings and imagine this happy place where only the math actually matters.

In this ideal world, we can now recall how we multiply two matrices together, as this. As we can see, we go across the row in the first matrix and then down the column of the second. In effect we can also see that the dimensions of the matrices must match up in a particular manner:

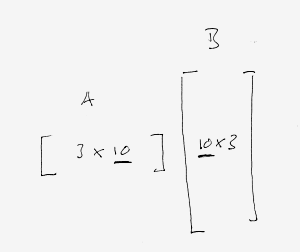
Shows how we can multiply two matrices of different dimensions as long as the inner dimensions match up (10 columns hitting 10 rows from the left).

This leads to the fact that we can multiply matrices of different size, as long as the inner dimensions match up. In the extreme case we can have one of the matrices have the outer dimension of one. This is effectively a vector! This leads us to the question, how do we represent a vector? We can either have a 1x3 matrix - we're going to call this a row vector - or a 3x1 matrix - we're going to call this a column vector. The dirty secret is that it doesn't matter too much, but you might want to consider following the right crowd here. There are two camps, people with math and physics backgrounds will usually have a preference towards column vectors and as I've noticed there are several graphics people who prefer the row vector notation. The one argument for column vectors is really that most math texts you will encounter will have column vectors in them. Swimming against the stream here will get you into trouble at some point just since you have to "translate" everything to your own engine format. Depending upon how proficient you are, and how many people you are on the team, this might or might not be an option.

One of the things you might see is that it's far easier to write a row vector in text, much like this [a b c] instead of a column vector, since it needs to be written like this 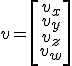. Often you will see that in texts we transpose the vectors, like this [a b c]^T. There is also an alternative notation, with an apostrophe like this: [a b c]^'.

There is one small theorem we need before starting to talk about the transforms and that is how transposing matrices fit together. If we have two matrices, the following holds true:

(eq 1) Transposing a multiplication.

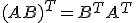
For now you can just take it on faith, with me waving my hands. Or you could look it up here.

Let us also introduce a convention so that we can name elements in a matrix. Let mij be an element in a matrix M. Then i refers to the row and j refers to the column in the matrix:

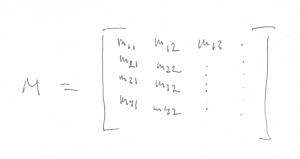
Shows the different matrix elements in a matrix. Note that the two subscripts are in the row, column order.

The final words to say in this section is that everything that we have covered here is conceptual, things that only work in our heads and on pen and paper. It doesn't necessarily work on computers.

Transformations

Most of the time in video games we don't have generic matrices, more times than not we have one particular matrix, a 4x4 homogeneous matrix describing a transform from one space to another. Now we suddenly can identify the elements in the matrix as having meaning. We recall that a typical transformation matrix that takes us from one space to another typically (omitting scale and projection) needs a basis and a translation. For us, a basis consists of 3 axes spanning the room. A typical matrix might look like:

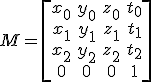
So how did we arrive to this? Typically to go from one space to another, we need to project the local space positions onto the basis to get the new positions. So for our example going from the space described by M with a local position p to get a point in the parent space as q, we need to:

q.x = x * p + t.x
q.y = y * p + t.y
q.z = z * p + t.z

Basically what this does is to project the local space point onto the spanning axes and then add the translation to the components. This very neatly can be represented as the above matrix if we make sure that the last component of p is 1 and that the p vector is a column vector. It's pretty easy to see that if we apply eq 1 we get the case with a row vector, where we get that:

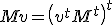
Transposed multiplication using eq. 1.

This shows how the transformation matrices must be composed for column and row vectors. Note how the post/pre multiplication falls out of the multiplication rule for matrices. So saying that we have the notation of column/row vectors implies a certain arrangement of the matrix and also the multiplication order.

Next, computers

Now, let us leave the nice ideal place where math is absolute and enter the land of computers. Now suddenly we need store the elements of the matrix in memory. Unfortunately it's not universally defined how to do this. There are two major ways to do this. If you have the ideal matrix and it's elements and want to store it in a flat memory array you can either do it like this:

Column major storage mode

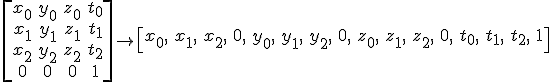
or like this:

Row major storage mode

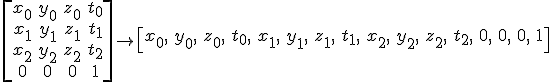
See how this concept is completely orthogonal (separate) from the concept of the column/row vector notation? To put this to test, we can see what happens with a typical transformation matrix if we have first a column vector and column major storage mode:

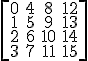
The indices indicate the flat storage index in memory of the different elements of the matrix. Note that the translation will be placed in the last column and will wind up in memory array indices 12,13,14 and 15.

and now if we have row vectors with row major storage mode:

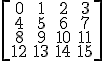
The indices indicate the flat storage index in memory of the different elements of the matrix. Note that the translation will be placed in the last row and will wind up in memory array indices 12,13,14 and 15.

Notice how the element in the resulting array falls in the exact same order for both cases?

The important distinction here to note is that whenever we talk about column/row major matrices, we are talking about their storage. Whenever we talk about row/column vectors, we are really talking about what element in the matrix means what and in which order we multiply a matrix and a vector.

That paragraph was really the gist of this whole article. Read it again.

Why choose either?

So there are two ways to pack things. Can we just choose one and be done with it? Turns out it's not as clear cut as that. On the CPU chances are that for single matrices you are probably going to ask it questions like "what's the translation?" or "which way is forward?". Both want to read a resulting vector and it would be nice if that vector was readily available without gathering it from a scattered representation, say for example if we had chosen to have row major matrix packing and column vectors.

So for the CPU most of the time it makes overwhelming sense to keep it simple and have matching concepts of vectors and the matrix packing (column vectors with column major packing). However if we move to the GPU, we often just want to transform vectors with the resulting matrix at which point it's much more advantageous to have store the matrices transposed so that we simply can do a couple of dot products. In the case for when we have simple affine transformation, we can skip the fourth row/column and save one register on the GPU. A simple transformation would look like this:

#pragma pack_matrix (row_major)
float4 pos;
float3x4 bone;

q = mul(bone, pos).xyz;


// HLSL row major assembly (uses 3 constant registers)
dp4 oC0.x, c0, v0
dp4 oC0.y, c1, v0
dp4 oC0.z, c2, v0

// HLSL column major assembly (uses 4 constant registers)
mul r0.xyz, c1, v0.y
mad r0.xyz, c0, v0.x, r0
mad r0.xyz, c2, v0.z, r0
mad oC0.xyz, c3, v0.w, r0

// Cg row major assembly (uses 3 constant registers)
DP4R  o[COLR].x, f[TEX0], bone$0;
DP4R  o[COLR].y, f[TEX0], bone$1;
DP4R  o[COLR].z, f[TEX0], bone$2;

As you can see I've forced the matrix packing order with a pragma, which is standard in HLSL. Cg just have row major packing, which in most cases makes sense.

In closing

So the reason why all of this is really important is that dealing with matrices you can always if you don't know what you're doing fiddle a little bit until it looks right. The problem is that two wrongs doesn't make a bigger puddle of mess, but it can turn out seemingly correct. For example, incorrectly transposing the matrices and then choosing the wrong memory layout will actually result in the correct behavior, but the logic in between is wrong. It will manifest itself if someone (or you) else is trying to add some extra things in the middle. Even though they can do it correctly, now suddenly things might not work out as expected anymore since the parity of the errors got thrown off.

The only parity of errors that works is 0. All others are really illusions and should be hunted down, skinned and jumped upon up and down a couple of times for good measure.

Finally, the guidelines for your matrices would be: think of your vectors as column vectors and thus have the spanning axis of your room in the columns of the matrix, multiply the matrices with the vectors as M * v. Store you matrices on the CPU as column major and on the GPU as row major.

Resources

Here are some more articles on the whole subjects, I guess it has been reiterated a couple of times and I am adding to the flames here. Although, note that some of the articles in these links actually gets it slightly wrong, or at least confuses things.